In earlier posts we have set the foundation for hedging in practice. We did this by calculating Option Price Sensitivities (Greeks) and Delta hedging for European Call as well as Put Options. Why would you want to hedge Gamma?
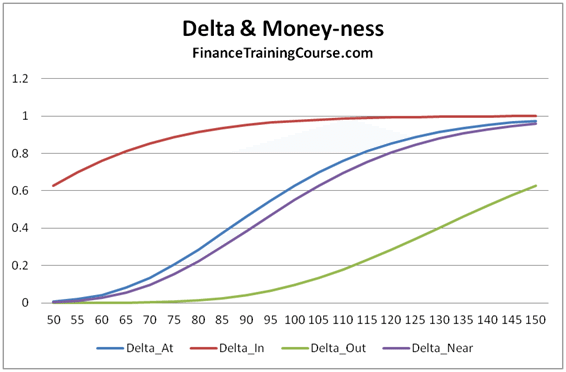
Figure 1 Options Greeks – Delta and Moneyness – Hedging higher order Greeks
If you leave it un-hedged you are exposed to the risk of large moves, especially when the option is at or near money. When you are deep out or deep in, Delta is flat and asymptotic as shown above. But when are you not, a large move can result in significant trading loss despite being Delta hedged. As long as prices move in small increments and do not jump dramatically, Delta hedge will cover you. The underlying jumps, you are exposed. We have seen this at work earlier with duration and convexity with similar implications. Delta is the first order rate of change and works well within a narrow band. Within and outside that band Gamma tracks not just the error but also the magnitude of your gain/loss in case of a large move (up/down). The magnitude of the error shifts dramatically as the option gets closer to the At/Near money state. When options are deep in or deep out, similar to Delta, Gamma also flattens out. However given the convex nature of the 2nd derivative in this case, the impact of a large up move or a large down move is not symmetric.
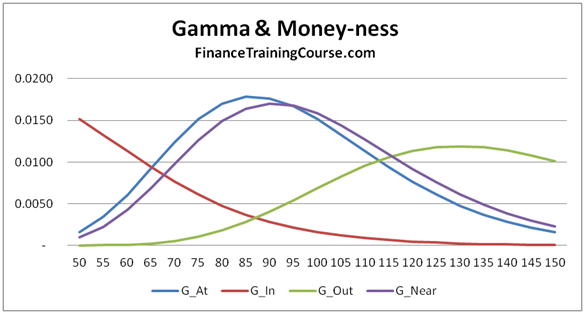
Figure 2 Option Greeks – Gamma & Moneyness – Hedging Higher order Greeks
But you can’t hedge higher order Greeks (Gamma) by buying or selling the underlying. Why not? First the 2nd derivative of a spot/forward/linear position is zero so hedging Gamma through the underlying is out. The second complexity arises with Vega. We really don’t know what shape or form realized volatility will take in the future. How can we effectively hedge it? Then there is the issue of term structure of volatility. Implied volatility changes based on time to maturity (term structure) as well as money-ness (deep in, deep out, At/Near – strike price) so taking a simple constant volatility view across all options irrespective of maturity or money-ness would actually be in-accurate.
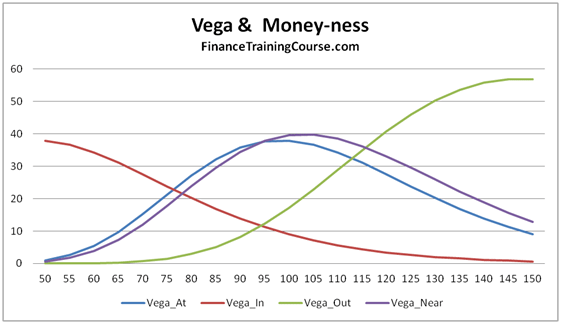
Figure 3 Option Greeks – Vega & Moneyness – Hedging higher order Greeks
The third catch is that both Gamma and Vega use exactly the same calculation function for Calls and Puts (Gamma for a call and put has the same value, Vega for a call and a put has the same value). Which creates interesting implications for hedging a book of options with calls and puts. You may be perfectly hedged and squared with respect to your Gamma and Vega exposures but the wrong universe/direction of hedging choices can still wipe you out. We hedge Gamma and Vega by buying other options (specifically cheaper out of money options) with similar maturities. Like Delta hedging we need to rebalance but the rebalance frequency is less frequent than Delta hedging. Your final hedge is therefore a mix of exposure to the underlying (partial delta hedge) and cheaper options with similar maturities. The only question is that it’s a large universe of options out there, how do we manage multiple constraints including premium & sensitivities across products, maturities (tenors), Delta, Gamma & Vega. The answer is constraint optimization through Excel solver. In our next series of posts we will show how to build a simple Excel solver model that takes a universe of options and uses it to match the required Delta, Gamma, Vega profile for a single option as well as a portfolio of short positions.
- Lesson One – Hedging Gamma and Vega – Introduction
- Lesson Two – Hedging Gamma and Vega – Building the Solver Model
- Lesson Three – Hedging Gamma and Vega – Solver Solution review
- Lesson Four – Hedging Gamma and Vega for a book of options
- Lesson Five – Hedging portfolio Vega and Gamma using solver
However before you jump to this series of lessons, please review the following background posts on Option Greeks & Delta Hedging to ensure that you are comfortable with the calculation of Delta, Gamma & Vega as well the implementation of Delta Hedging in Excel.

Comments are closed.