Convergence between closed form and simulation model prices is enhanced with variance reduction procedures. It encourages model extension to complex products. For our TARF pricing model in its original form convergence is a challenge. We will try and address that challenge in this post by identifying a few legitimate Excel convergence hacks that we can use to speed things up without adding two much computational complexity or computational horsepower.
The Antithetic Variable Technique is one variance reduction procedure that ensures faster convergence to the deterministic closed form results. The procedure involves calculating two values for one simulation trial. One value is derived using the usual MC simulation method while the other value is calculated by changing the sign of all the random samples from the standard normal distribution used for determining the simulated spot series. The two values of the derivatives are then averaged for the simulation trial. The estimate of the value of the derivative is the average of these average values across all simulation trials. For a more in-depth look at the Antithetic Variable Technique and other variance reduction procedures see the post:
In our previous post on TARF pricing we compared the results obtained from our MC simulation models and the closed form formulas. We noticed that when we used a path dependent series of simulated Spot prices, the results showed a significant degree of variance from the results of the closed form formulas.
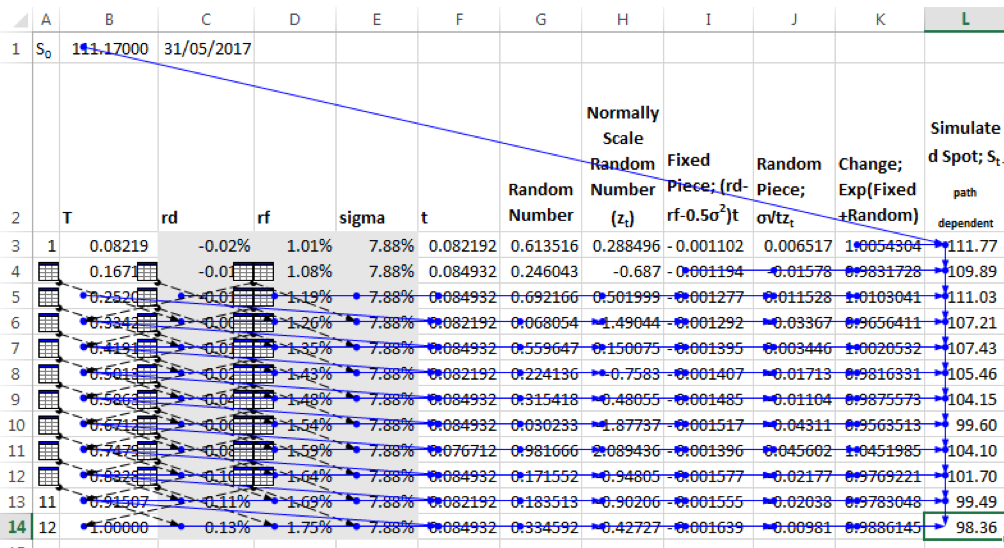
The screen shot below shows the path dependent simulated spot series. The simulated spot for leg 12 is dependent on the simulated spot for leg 11. The simulated spot for leg 11 is dependent on the simulated spot for leg 10 and so on. In general, the simulated spot for each leg is based on the simulated spot of the prior leg.
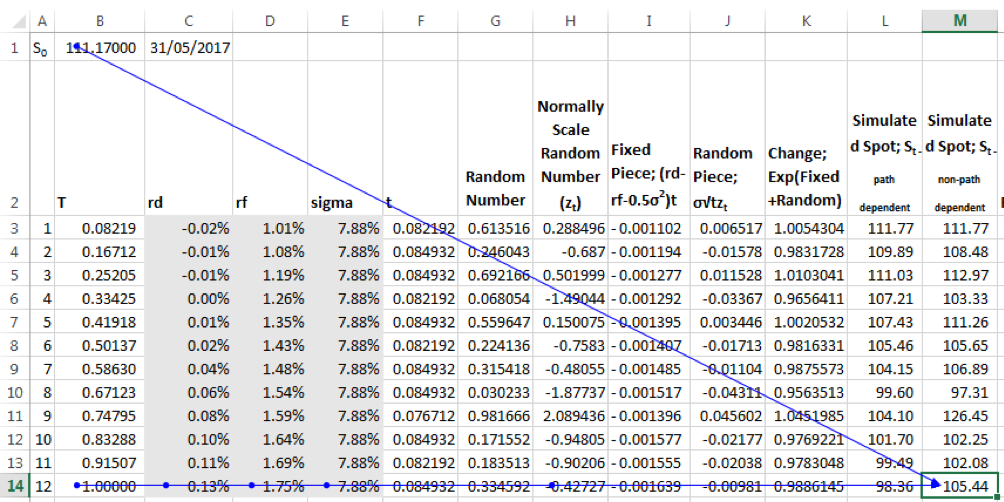
In contrast, a non-path dependent simulated spot series treats each leg independently. The Spot at each leg is evaluated based on the initial spot rate and does not depend on the simulated spot of the prior leg.
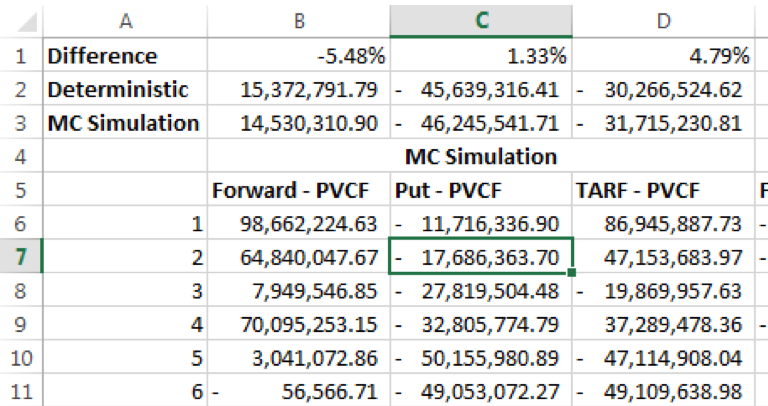
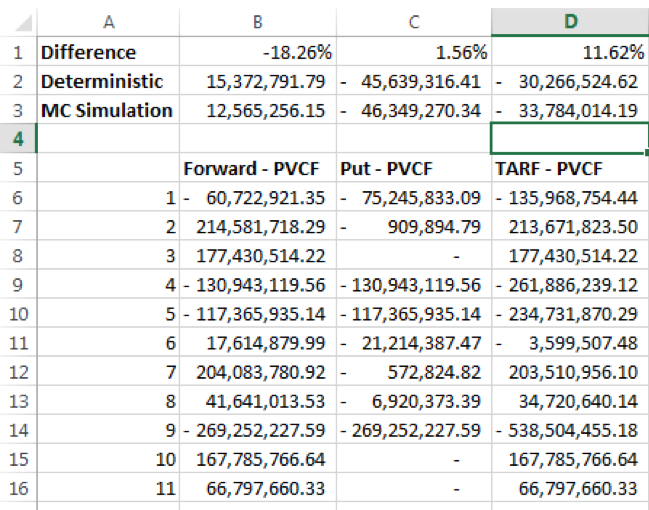
Using the non-path dependent series we noticed that the difference between the closed form and simulation results was reduced to a certain extent. This makes sense given the fact that each leg of the TARF may be considered a separate and independent forward and/or option contract – the entire product being a series of independent contracts. The screenshot below gives one estimate of the value of the TARF using the non-path dependent simulated Spot series.
The differences are still significant. To reduce the difference, and ensure a faster convergence to the formulaic results, we applied the Antithetic Variable Technique.
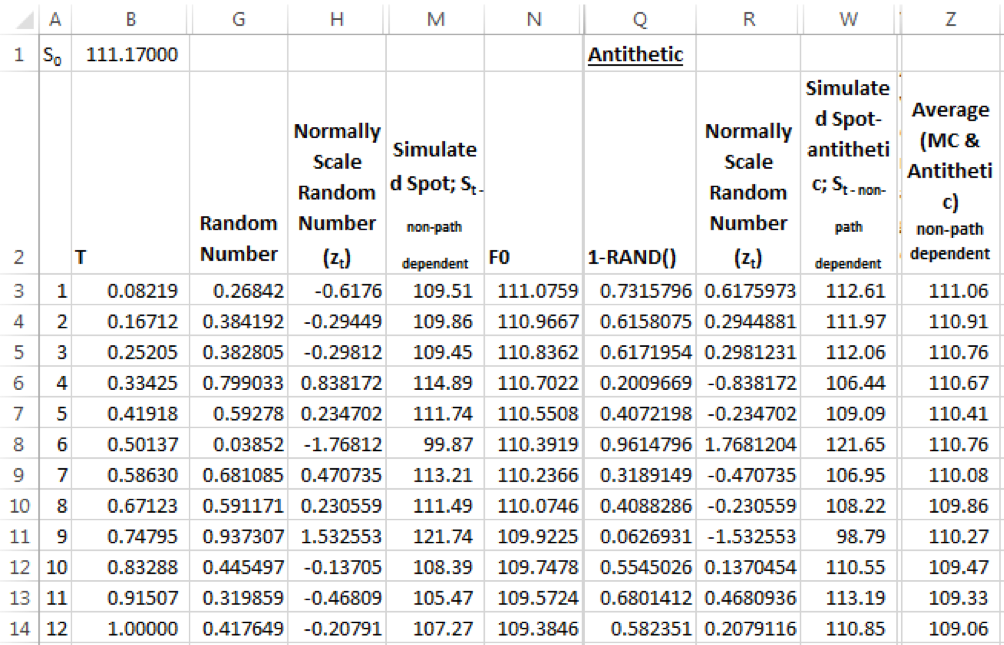
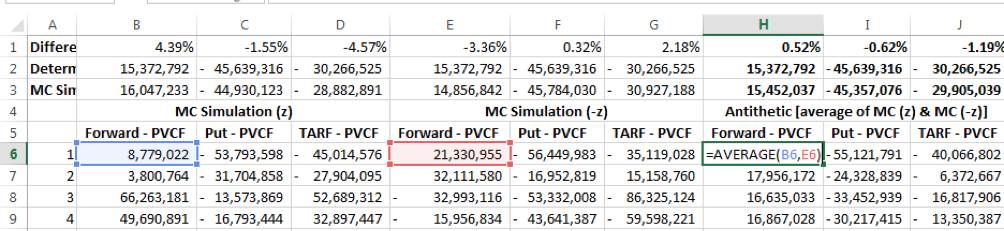
We recalculate the non-path dependent simulated spot series using the random series 1-RAND(), where the EXCEL RAND() is the random series from the uniform distribution used in the usual MC simulation approach. This in effect changes the sign of the random samples from the standard normal distribution from z to –z.
In the screen shot above M gives the spot series using the regular MC simulation approach, while W shows the results using the random samples with sign change (column R values are -1 x column H values).
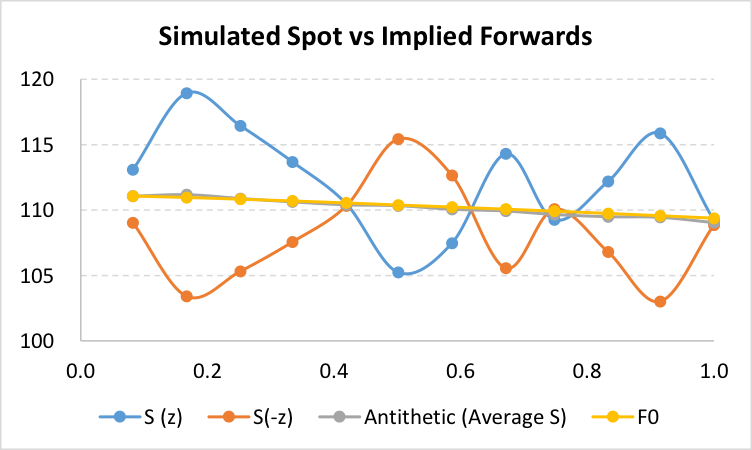
For the purpose of illustrating the impact of the convergence only, we look at the average of columns M & N (in column Z) and we can see that the results are much closer (almost superimposed on) to the implied forward rates used in deterministically valuing the forward contracts.
Note that these average values in column Z are not used in the model. The derivative values using the spot series in column M & column N are calculated and stored separately for each run as seen in the screenshot below. The average of these values is calculated for each simulation run.
The simulation model’s estimate of derivative value is the average of these average values across the 1000 simulation runs:
Using the same number of simulation trials, the results using the Antithetic approach are significantly closer to the closed form solutions.