We quite often use leverage to improve returns. When evaluating a business, it is important to assess underlying performance with as well as without the impact of leverage. To measure performance without the impact of capital structure, we need unlevered Beta or Asset Betas. This post will look at relevering Beta in WACC (weight average cost of capital).
1. Why do we need to relever Beta?
From a valuation perspective in a buyout opportunity there is quite often a dramatic change in capital structure, specially within Leveraged and Management Buy outs (MBOs and LBOs). Within this context, the current capital structure is not relevant to the buyer. Beta, therefore, first needs to be unlevered to get to Asset Beta. Then Asset Betas are re-levered again to test the impact of multiple debt levels (proposed capital structure) to find an optimal mix between risk, returns and debt pay down schedules.
When assessing the value of a company’s operation we discount free cash flows using the weighted average cost of capital (WACC). WACC or weighted average cost of capital is calculated using the cost of equity and cost of debt weighing them by respective proportions within the optimal or target capital structure of the company, i.e.
WACC = E/(D+E)*Cost of Equity + D/(D+E) * Cost of Debt, where E is the market value of equity, D is the market value of Debt.
The cost of debt can be observed from bond market yields. Cost of equity is estimated using the Capital Asset Pricing Model (CAPM) formula, specifically
Cost of Equity = Risk free Rate + Beta * Market Risk Premium
a. Risk components in levered Beta
Beta in the formula above is equity or levered beta which reflects the capital structure of the company. The levered beta has two components of risk, business risk and financial risk.
Business risk represents the uncertainty in the projection of the company’s cash flows which leads to uncertainty in its operating profit and subsequently uncertainty in its capital investment requirements.
Financial risk represents the additional risk placed on the common shareholders as a result of the company’s decision to use debt, i.e. financial leverage.
If capital structure comprised of 100% equity then beta would only reflect business risk. This beta would be unlevered as there is no debt in the capital structure. It is also known as asset beta.
2. How do we relever Beta in WACC?
To obtain the equity beta of a particular company, we start with a portfolio of assets of that company or alternatively a sample of publicly traded firms with similar systematic risk. We will first derive the betas of these individual assets or firms from market prices. The derived betas are levered betas as they would reflect the capital structure of the respective firms. They have to be unlevered so as to only reflect their business risk components.
From the unlevered betas, obtain a weighted average unlevered beta using as weights the proportions of the assets in the company’s asset portfolio or derive an average across all comparable firms. The weighted unlevered beta thus obtained would now be relevered based on the capital structure of the company in order to determine the equity or levered beta for the company. This beta would reflect not only the business risk but also the financial risk of the company.
a. Practitioner’s method vs Risky-debt formula
Unlevering and relevering beta in WACC may be done in a number of ways. A method employed by practitioners gives the relationship between unlevered and relevered beta as follows:
Levered Beta = Unlevered Beta * (1+D/E), where D/E = Debt-to-Equity Ratio of the company.
The practitioner’s method makes the assumption that corporate debt is risk free. If we consider corporate debt as risky then another possible formulation for relevering beta in WACC is:
Levered Beta = Asset Beta + (Asset Beta – Debt Beta) * (D/E) where we estimate Debt Beta from the risk free rate, bond yields and market risk premium.
b. Considering Taxation
The above formulations do not incorporate the impact of corporate taxation, i.e. the fact that debt returns tend to be tax deductible. In order to consider the impact of taxation the following adjustments will be made in the relationships given above:
Under the practitioner’s method:
Levered Beta = Unlevered Beta * (1+D*(1-T)/E) where T is the tax rate.
Under the risky-debt formulation:
Levered Beta = Asset Beta + (Asset Beta – Debt Beta) * (D/E)*(1-T).
And WACC would be equal to E/(D+E)*Cost of Equity + D*(1-T)/(D+E) * Cost of Debt.
c. Example
BetaCorp is a corporation that has two primary business lines – personal hygiene and consumer off the shelf pharmaceuticals. We are estimating its levered beta for the purpose of determining its cost of equity. The personal hygiene subsidiary is worth USD 20 million while the consumer pharma subsidiary is worth USD 30 million. The firm has a debt-to-equity ratio of 1. Assume that the tax rate for all firms is 30%. The risk free rate is 7% and the market risk premium is 6%. The following information is for firms with comparable systematic risk:
| Comparable Firms | Average Beta | Average D/E Ratio |
| Personal Hygiene | 0.9 | 20% |
| Medical | 1.2 | 60% |
Note that the average betas above denote the average of the levered or equity betas of these firms.
In the first step we will calculate the unlevered betas for each group of firms using the practitioner’s method:
Unlevered Beta for the personal hygiene business = 0.9 / (1+ 0.2*(1-0.3)) = 0.79
Unlevered Beta for the consumer pharma business = 1.2 / (1+ 0.6*(1-0.3)) = 0.85
The Beta for BetaCorp will be the weighted average of unlevered betas where the weights are in proportion to the subsidiaries value in the firm, i.e.
Unlevered Beta for BetaCorp = 0.79*20m/50m+0.85*30m/50m = 0.82
Levered Beta for BetaCorp = 0.82*(1+1*(1-0.3)) = 1.40
Cost of Equity = 7%+1.40*6% = 15.39%.
d. WACC, Beta and Market Risk Premium – Industry specific
We can extend the same model to calculate industry specific WACC estimates.
For instance, the figure below shows the calculation for US regional banks, the Computer Services industry and Energy and Power sector using the January 2016 data set shared by NYU and Dr. Damodran on their site.
i. Regional Banks
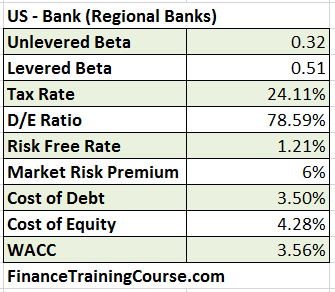
We have used the default 6% estimate (2015) for Market Risk Premium for all three industries.
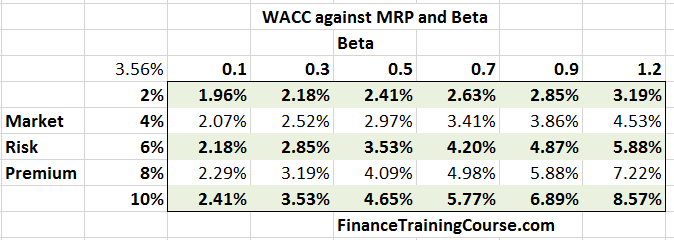
A quick sensitivity test of WACC by changing values of Beta and Market Risk Premium shows a range of WACC values between 1.96% – 8.57% for regional banks in the US. This range can become a third input in our in-class valuation intuition exercise
ii. Computer Services
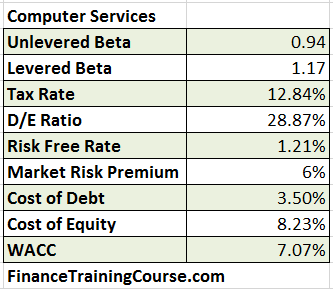
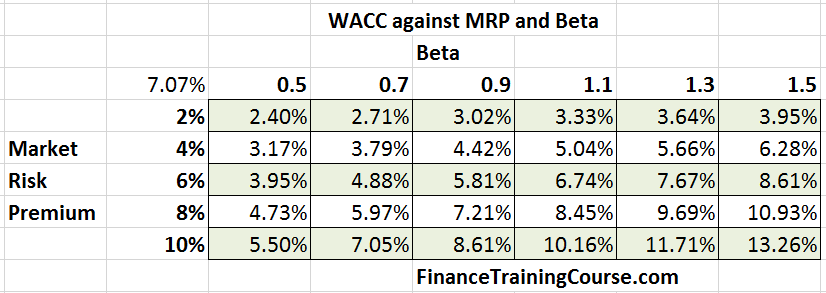
While we have used the same risk premium, different Beta and Leverage ratios lead to a different value of WACC for the Computer Services industry and the Energy and Power segment.
As expected a different WACC and a different relevant range because of change in WACC parameters.
iii. Energy & Power
WACC calculations for Energy and Power sector.
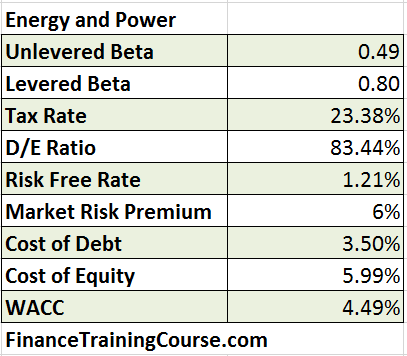
Sensitivity analysis for Energy and Power sector.

We can now use these estimates as part of our valuation exercises and case studies such as:
If you have an interest in using Beta and Alpha outside of the valuation and WACC world, such as in portfolio construction, portfolio allocation and portfolio optimization models see:

Comments are closed.