For our portfolio model we need an objective function that allows us to minimize the cumulative Greek gap across maturity buckets with respect to Vega and Gamma between the short positions and the proposed hedge portfolio.
We will try two alternates. In the first instance we calculate cumulative gap and use that as the objective function. In the second instance we keep the constraints around gap by maturity but switch to a different objective function to see if Solver can still find the correct solution.
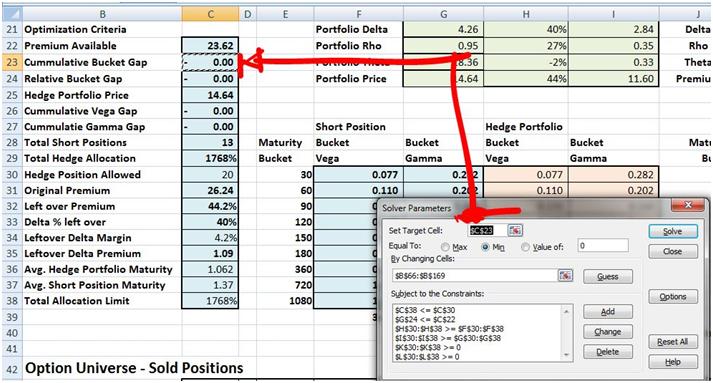
Figure 1 Hedging Vega & Gamma – The Solver objective function
A word about cumulative bucket gap and the constraints used in the Solver model before we proceed.
Our first objective function is a value that summarizes the differences across 18 different cells in four separate steps. Let us review these steps.
The objective function as shown above is defined in cell C23 (tagged as step
(1) in the image that follows). C23 is a summary cell linked to cell K40 (tagged as step
(2)). K40 is the sum of K39 and L39 which in turn sum up the Greek gap differences by maturity bucket in the K and L columns immediately above (tagged as step (3)). The differences are calculated by comparing the portfolio Greeks for the original short position and the hedge portfolio in column F,G,H & I (tagged as step (4)).
Even though the objective function appears to be one cell, its value is driven by differences that exist across four columns summarized in two additional columns summarized further in two cells finally linked to a single cell. This approach doesn’t always work within Solver but luckily for the higher order Greeks hedging problem, it does.
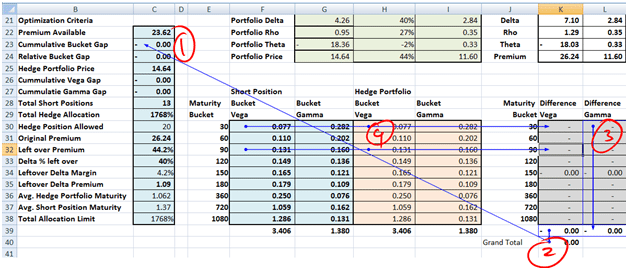
Figure 2 Hedging Gamma & Vega. Understanding the objective function components.
The reason why it does and why we may be able to play with other definition of the objective functions are the constraints used in the setup of the problem in Solver. There are four column constraints in the Solver model.
Hedging Gamma & Vega. Constraints review
The first two H and I column constraints shown below specify that the hedge portfolio Greeks (Vega and Gamma) should be atleast as high as the short position Greeks.
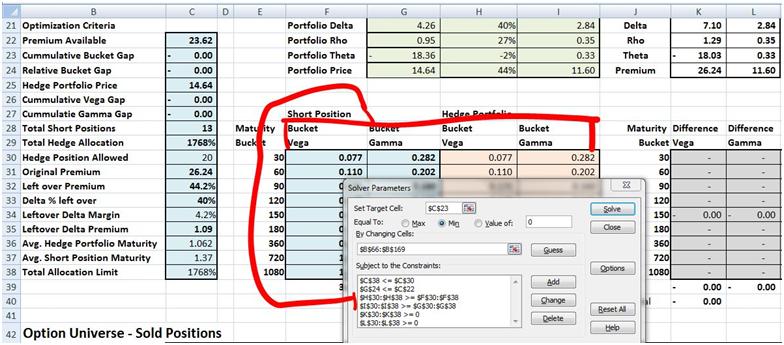
Figure 3 Hedging Gamma & Vega – The first two constraints
The next two (column K and L) require that Greek differences in each maturity bucket amount to zero. There is some element of redundancy here but once we have found a solution we can play with the constraints to see which one is required and which one is redundant.
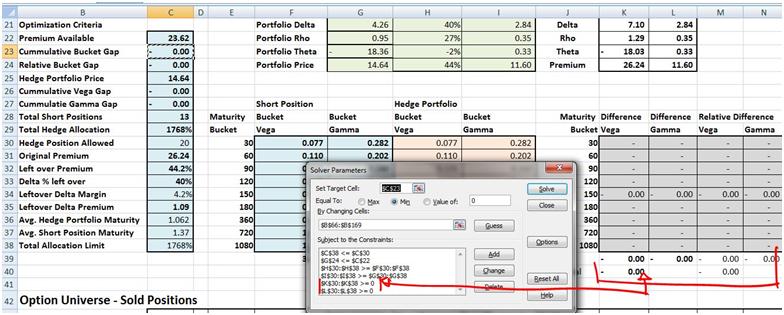
Figure 4 Hedging Gamma & Vega – the last two constraints
The first two single cell constraints ensure that we don’t spend more than what we have (premium available) and force hedge portfolio allocation across multiple positions.
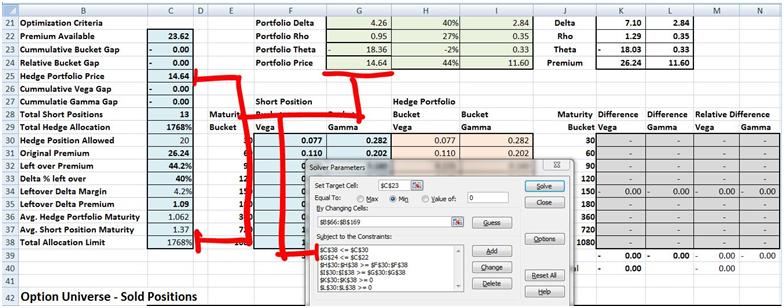
Figure 5 Hedging Gamma & Vega – Premiums and allocations
Hedging Gamma & Vega. Solver Solution – First pass
Our first solution does a reasonable job of hedging Gamma and Vega exposure but appears to be a bit pricey compared to the solutions we had seen in our simpler model.
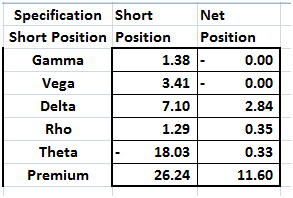
Figure 6 Solver Solution – First pass
Maturity buckets also perfectly offset
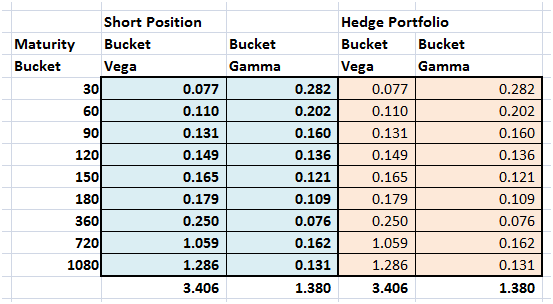
Figure 7 The two portfolios side by side
The differences grid also sums up to zero.
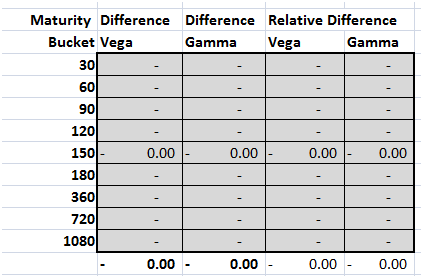
Figure 8 absolute & relative differences
However when we review the portfolio allocation we run into issues. The first is the number of options used to hedge the short portfolio. There are 29 individual positions to hedge our 13 short positions across 9 maturity buckets. We would like to see if we can reduce the number of positions as well as the cost of our hedge portfolio by playing around with the objective function and the constraints.
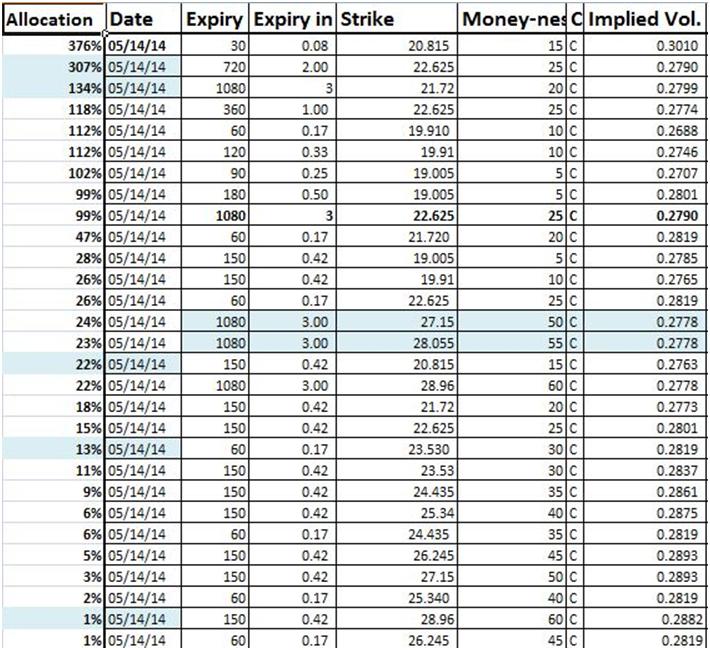
Figure 9 The hedge solution allocation – first pass
Minimizing hedge portfolio cost
To minimize hedge portfolio cost we will change the objective function. Previously we minimized cumulative bucket gap. In this iteration we will minimize the cell representing hedge portfolio cost. We will also remove the additional constraint around total portfolio allocation to give Solver the freedom to move around our hedge universe and pick as many positions it needs to come up with a more cost effective solution.
Here is what the revised Solver model looks like.
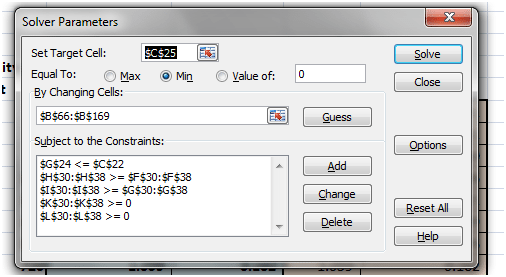
Figure 10 Solver Model – Minimize cost
Note that we are short of one constraint and the objective function has changed. We press Solve and solver finds a solution.
The maturity bucket grid is a match
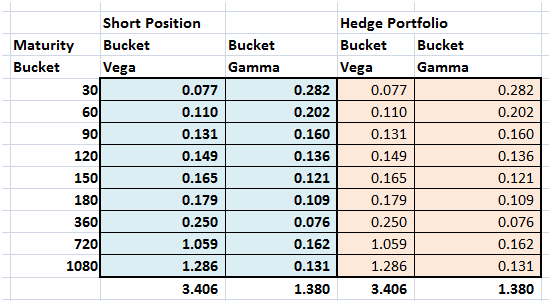
Figure 11 Minimize cost – Maturity bucket grid
The differences grid adds up to zero.
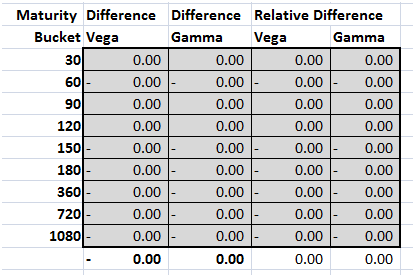
Figure 12 Relative differences grid – Second pass
The hedge portfolio cost has also declined from our earlier $14.64 to $9.62 dollars
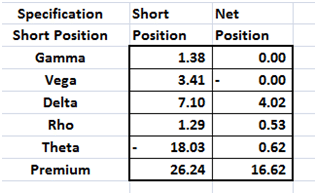
Figure 13 Solver solution – optimized for lowest hedge cost
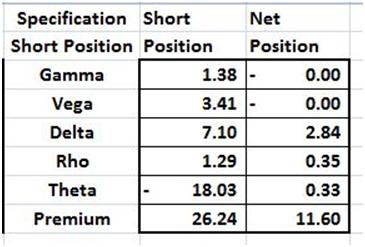
When we put the two solutions side by side, we see that while Gamma and Vega remain perfectly hedged Delta, Rho and Theta un-hedged exposures have risen. However the premium saving of 5 dollars adequately compensate us for this change.
Our next question deals with redundant constraints.
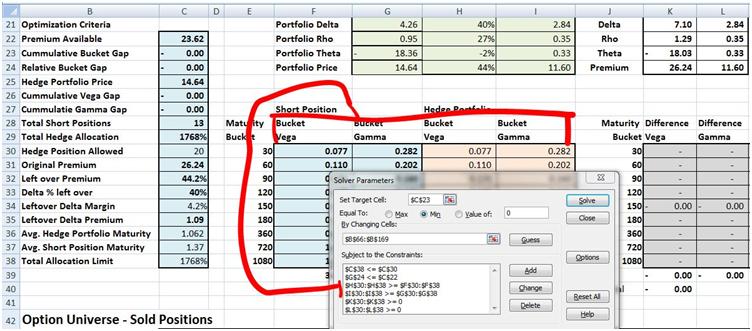
Figure 14 Solver model – redundant constraints
Do we really need the four column constraints (maturity buckets, difference by maturity buckets)? Can we just get by with two rather than four? We go ahead and drop both (Vega and Gamma) the maturity bucket grid constraints assuming that the difference by maturity bucket constraints should be sufficient to reach a solution. The answer is unfortunately no.
Rather than adding both Gamma and Vega buckets constraints together, we add the Gamma bucket first and then solve and reach a solution quite close to our second pass. There is a marginal difference in premium over our previous solution. So we do need Vega bucket constraint to solve for the optimal solution.
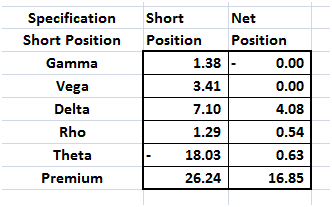
Figure 15 Solver solution – Optimal results grid
However a bigger issue now is the number of positions required to hedge the portfolio. While our new and improved solution is certainly cheaper than our first pass, there are now 86 positions required to hedge our 13 short call positions.
We add a new constraint that restricts the number of positions first to 30 and then to 50. However in both instances a feasible solution is not found.
However when we increase the limit to 55 a feasible solution is identified and it comes with an added bonus of lower cost.
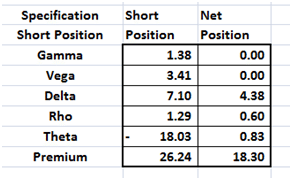
Figure 16 Solver solution – side by side comparison
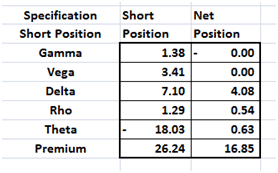
Number of positions are down to 52, premium is down to 7.94 from 9.62 earlier.
Optimizing Delta
Let’s now look at the solution with a slightly different point of view. While our Gamma and Vega exposure stays perfectly hedge, hedge premium cost and left over Delta exposure goes up and down in an inverse manner. Premium cost comes down, Delta goes up. Delta goes down premium cost goes up. Rather than minimize premium we would like to see if we could find an optimal solution that would also balance the left over Delta amount side by side with our Gamma and Vega hedging solution.
So we create a new objective function that focuses on Delta and run Solver again.
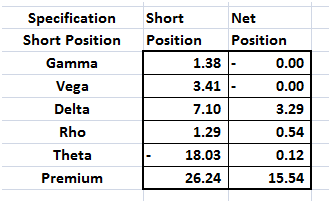
Figure 17 Optimizing Delta hedge
Interestingly enough in this solution it’s not just Delta that comes down but the number of position required to hedge our exposure also drop from 52 all the way down to 26 with about 11 major positions and 15 minor exposures. However premium jumps up from seven dollars and change to ten dollars and change. Playing with the model allows you to push Delta all the way down to 1.9 at a cost of $19.
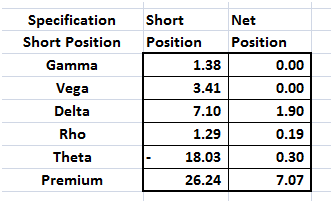
Figure 18 Optimizing Delta – second pass
Here is what the revised portfolio allocation looks like for Delta at 3.9, premium at $10.4
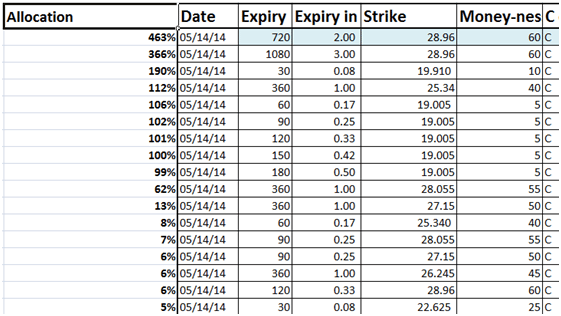
Figure 19 Revised allocation
Compare this to the optimal solution at $7.94 with 53 positions.
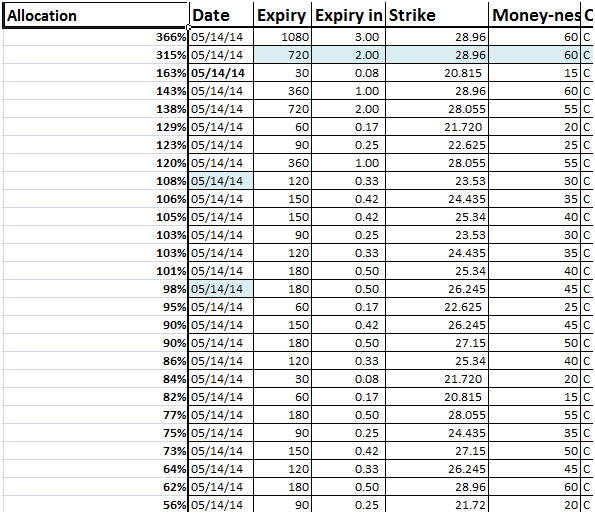
Figure 20 Optimal allocation – final pass
The two solutions should point out an obvious lesson. Shorter dated options are more sensitive to changes in the price of the underlying and less sensitive to changes in implied volatility. Longer dated options are more sensitive to changes in implied volatility.
To find the optimal solution you need to find the right balance between the two. Which within our limited setting Solver does reasonably well. Any leftover Delta exposure can then be hedged using the Delta hedging models we have discussed earlier.
Once again all of these variations were discussed to build a better understanding of Vega and Gamma. We are sure that many additional tweaks are possible. If you would like us to try more variations, please feel free to suggest them. We would be happy to accommodate them.
In case all of the above was akin to a Greco-Roman tragedy for you, here is a list of earlier lessons in the series that you can use to decode the language.

Comments are closed.