Pricing a financial instrument is not an exact science. There may be formulae, mathematics, derivation, proofs and exact models but in essence pricing financial securities in real-world markets is more along the lines of a science of approximation.
One approach to pricing these instruments is to use a Monte Carlo Simulator. A simulation is an experiment, and an MC simulator may be considered a machine that can churn out a series of experiments. The simulator will behave in a certain fashion (i.e. produce symmetric, asymmetric, normal and skewed, with thin tails or long fat tails) depending on the tool used to build the machine (i.e. the choice of distribution). By definition, it will always be inaccurate and an approximation to the real world.

What are the prerequisites?
A useful introduction to some of the concepts mentioned in this roadmap are the following online courses:
What topics are covered?
How can I build Monte Carlo Simulators in EXCEL?
The Monte Carlo (MC) simulation concept is best explained through example and in the following courses, we explain basic MC principles by building simulators in EXCEL for currencies, commodities and equities. We also explain the link between increasing the number of trials and increasing the accuracy of simulation results:
- Computational Finance: Building Monte Carlo (MC) Simulators in Excel
- Convergence and Variance Reduction Techniques for Option Pricing Models
The following post suggests a solution for addressing the normality assumption challenge by replacing the normal distribution with the historical distribution.
What are some applications of Monte Carlo Simulations that I will learn?
In the next stage we consider Monte Carlo simulation applications:
- Interest rate modeling
- Option pricing
- Calculation of Value at Risk
- Pricing Ladder Options using a Monte Carlo simulator
- Pricing Exotic Options – Asian, Look backs, Barriers, Choosers
- Delta Hedging Applications
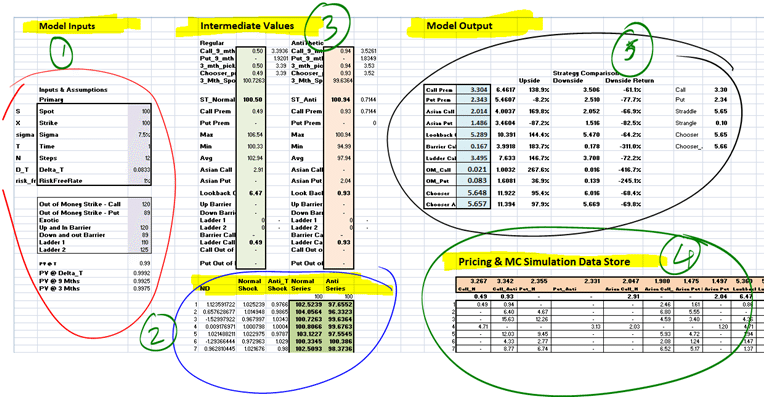
What are the additional topics I can read up on?
- Option pricing using Binomial Trees
- Derivative products
- What is N(d1) and how is it different from N(d2)?
- Interest Rate Simulation Crash Course
Case Studies
Premium Content
- Cox-Ingersoll-Ross (CIR) Interest Rate model – EXCEL example
- Calculating VaR for Futures and Options – EXCEL
- Exotic Option Pricing using Monte Carlo Simulation
- Monte Carlo Simulation – Models and Applications
- Monte Carlo Simulation – Equity – Example
- Monte Carlo Simulation – Commodity – Example
- Monte Carlo Simulation – Currency – Example
- Monte Carlo Simulator with Historical Returns
- Monte Carlo Simulation – with Option Pricing – Package
- Monte Carlo Simulation – Package
- Monte Carlo Simulation – Variance Reduction Procedures – EXCEL Examples
- Pricing Ladder Options using a Monte Carlo Simulator
- Understanding N(d1) & N(d2) – EXCEL Example
- Value at Risk using the Monte Carlo simulation with Historical Returns approach

Comments are closed.